Coordinate System
Before we jump into the coordinate system of MapLibre Native, let’s quickly review the concepts of translating a position on the face of Earth to a map tile. This is not a comprehensive refresher of coordinate reference systems or rendering basics. Rather this intends to guide the reader on what we want to achieve in this section.
We start from Earth, which is a geoid which is mathematically expensive to use as a reference coordinate system. Thus, we approximate the earth to reference ellipsoids or datum. For this documents’ scope, WGS84 is used as the canonical datum. Our goal is to represent geometries defined by WGS84 longitude, latitude pair coordinates to a map tile.
Instead of translating a full geometry, in the following subsections, we will project a WGS 84 point to a map tile rendered in MapLibre Native.
World vs Earth
This document uses the word Earth when it refers to the planet in which we all live in and make map tiles for. This document uses the word World to denote the world MapLibre Native renders. The word world in rendering terms mean the world to render. It could be a set of cones and boxes, a modeled city, anything composed of 3D objects. MapLibre Native renders map tiles in a range of zoom levels on a 3D plane. Map tiles are already produced from a WGS84 ellipsoid. Therefore, when this document uses the word World, it means the 3D plane containing a set of map tiles to be rendered, not the Earth.
Transformations
MapLibre Native requires a series of coordinate transformations to render a geometry from map tile. This is where we refresh our rendering knowledge a bit. To render anything through a GPU:
-
Design and define model in the Local Space. We call anything that needs to be renderer a model. In the Local space, a model lives in its own coordinate system. For MapLibre Native, in local space each individual tile is modeled. This map tile is already populated by a map tile generation process. The longitude, latitude bound per tile is now translated to pixel bounds in this local space.
-
When model matrix is applied to local space, as in a camera is applied, Local Space transforms to World Space. In this space, the model coordinates are relative to the world’s origin. In this space all the individual map tiles to be rendered are introduced in the world space.
-
The World Space is not seen from a viewpoint of a camera. When we see the world from a viewpoint of a camera, view matrix transformation is applied. Cameras can see the world up to a distance like human eyes can. To emulate that we apply Projection Matrix to View Space and end up in Clip Space1.
-
Finally, the World Space is transformed to device screen by applying viewport transform matrix.
Going forward, scoping our discussion only to MapLibre Native, we will talk mostly about two categories of coordinate systems:
-
World Coordinates
-
Device Coordinates
World Coordinates are defined in World Space. This speaks of how this world defines itself in a three-dimensional space.2 On the other hand, device coordinates are used through View, Clip, and Screen Space. The purpose of this set of coordinates is to define how the world will be projected on a screen. Device Coordinates define how a world will be projected on a screen.
The unit of measurement will be pixels in this document. When the map tiles are generated by a system, the unit of distance in each tile is measured in degree angles instead of meters. Because angular distance stays the same if we move the angle across the axis of earth.
Figure 2 shows rendering map tile through the rendering spaces and transformations below:
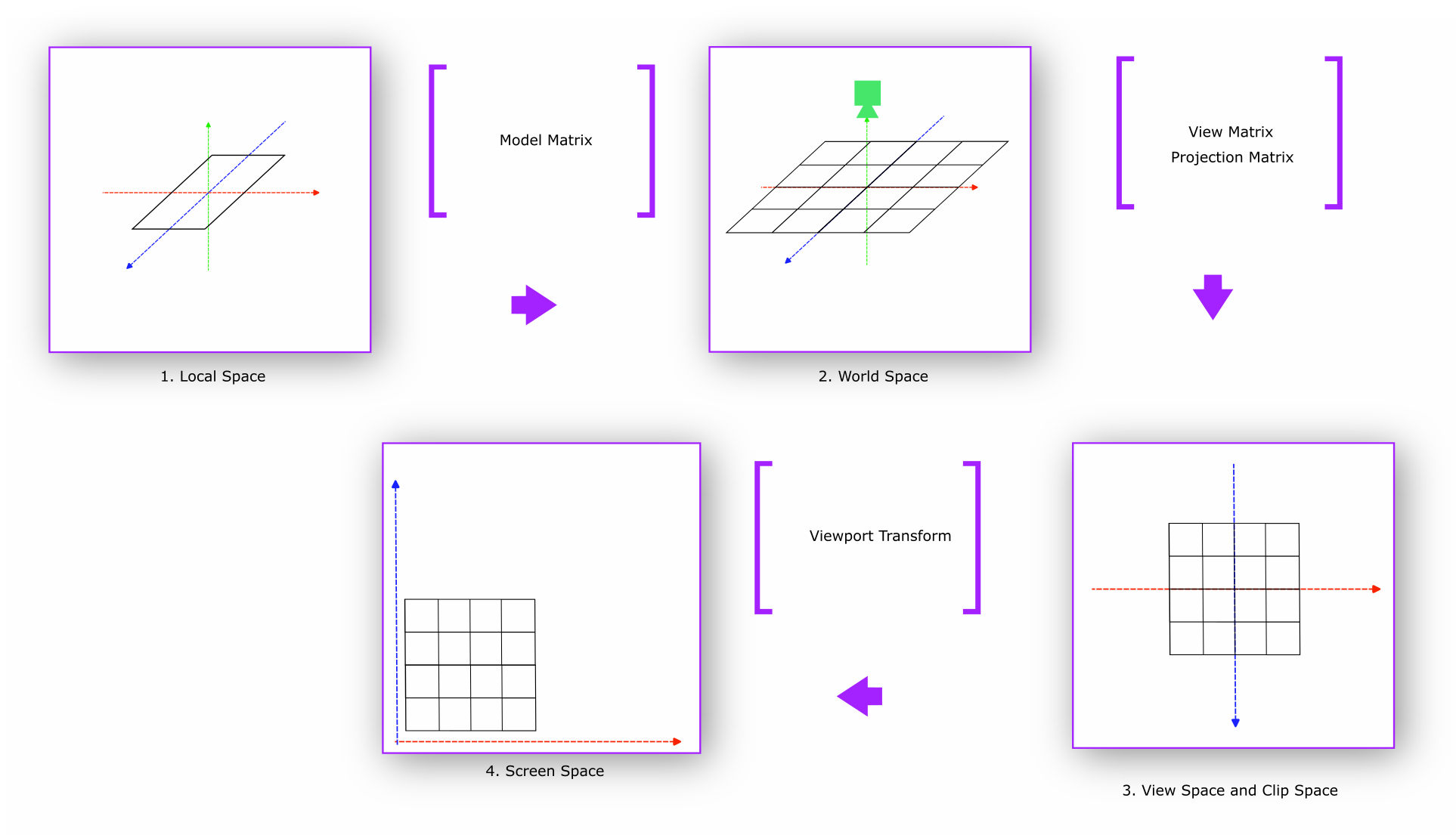 Figure 2: Rendering Spaces and Transformations for Map Tiles
Figure 2: Rendering Spaces and Transformations for Map Tiles
World Coordinates
World Coordinates for maps start with Geographic Coordinate Systems. Geographic Coordinate Systems use the three-dimensional model of the earth (ellipsoid) to define specific locations on the surface to create a grid. Traditional longitude, and latitude coordinate pair to define a location is an example of using geographic coordinates. EPSG: 4326 (WGS84) is the reference Geographic Coordinate System that most of the world’s geospatial data is defined and stored3 in. There is no way to visualize the WGS84 coordinate system on a two-dimensional plane, in this case, the map.
Projections are used to translate WGS84 coordinates to a plane. To be specific, projections are used to translate a location on the ellipsoid to a two-dimensional square. EPSG:38574 or projected Pseudo-Mercator Coordinate System is such a coordinate system. EPSG:3857 is used by MapLibre Native as a default coordinate system to display maps. This system takes WGS84 coordinates and projects them into sphere. This stretches out the landmass in the hemispheres but mathematically makes it simpler to project a location back to a 2D plane. As in, a sphere divided into angular equidistant grid produces rectangular grids when projected into a 2D plane. The philosophy behind this was to make rendering maps easy, as in drawing 2D squares on a plane is computationally trivial.
Our world can be now broken down into these squares or tiles as we will call it going forward. This system imagines the world as a giant grid of tiles. Each tile has a fixed size defined in pixels.
worldSize = tileSize * number of tiles across a single dimension
For brevity, this document assumes the reader knows that map tiles are divided into a range of zoom levels. And each tile in zoom N gets divided into 4 tiles in zoom N+1. A tile size of 512 pixels and zoom level 11 will deduce worldSize to be the following:
worldSize = 512 * 2^11 = 1048576
Although each tile breaks into 4 in the next zoom level, we used a power of 2. This is because X and Y both dimensions expand with a factor of 2.
Example: We start from translating a WGS84 location with longitude
-77.035915 and latitude 38.889814. To translate a degree longitude
relies on normalizing the latitude range [-180, 180] to [0, 1048576]. This means the X pixel value of a specific tile requires
shifting our coordinate by 180. For example, a location with longitude
-77.035915 becomes*:*
X = (180 + longitude) / 360 * worldSize
= (180 + -77.035915) / 360 * 1048576
= 299,904
Finding the X coordinate is easy to compute. But the Y requires a more than normalizing the range. This is due to the aforementioned space stretching in the hemispheres5. Latitude value (Y) defined in WGS84 will not be the same position after stretching. The computation looks like the following if the latitude was 38.889814:
y = ln(tan(45 + latitude / 2))
= ln(tan(45 + 38.889814/ 2))
= 0.73781742861
Now, to compute the pixel value for y:
Y = (180 - y * (180 / π)) / 360 * worldSize
= (180 - 42.27382˚) / 360 * 1048576
= 401,156
Tile Coordinates
Our next pursuit is to translate World Coordinates to Tile
Coordinates. Because we want to know where exactly inside a map tile a
location (longitude, latitude) coordinate gets rendered and vice versa.
This system creates different pixel ranges per zoom level. So, we append
the zoom level along with the X and Y pixel values. Dividing the pixel
values with the tile size normalizes the X and Y value per tile. This
means (x:299,904, y:401,156, z:11) becomes (585.7471, 783.5067, z11).
We divide our X and Y pixel value by tile size because we want to know
the starting coordinates of each tile instead of individual location
coordinates. This helps in drawing a tile. If we now floor the
components to integers, we get (585/783/11). This marks an individual
tile’s X, Y, and Z.
To reach our goal of translating a location to a coordinate inside a
tile, we need to know what is the extent of the tile. MapLibre
Native follows Mapbox Vector Tile (MVT) spec. Following said spec,
MapLibre Native internally normalizes each tile to an extent of
8192. Tile extent describes the width and height of the tile in integer
coordinates. This means a tile coordinate can have higher precision than
a pixel. Because normally a tile has a height and width of 512 pixels.
In this case, with an extent of 8192, each Tile Coordinate has a
precision of 512/8192 = 1/16th of a pixel. Tile extent origin (0,0)
is on top left corner of the tile, and the (Xmax, Ymax) is on the bottom
right. This means (8192, 8192) tile coordinate will be in the bottom
right. Any coordinate greater or lesser than the extent range is
considered outside the extent of the tile. Geometries that extend past
the tile’s area as defined by the extent are often used as a buffer
for rendering features that overlap multiple adjacent tiles.
To finally deduce the Tile Coordinates we multiply the remainder of our Tile components with extent:
(585.7471, 783.5067, z11) -> (.7471 * 8192, .5067 * 8192) = (x:
6120, y: 4151)
This makes the Tile to be (585/783/11) and Tile Coordinates
to be (x: 6120, y: 4151) for WGS84 location with longitude -77.035915,
and latitude 38.889814.
After defining Tile Coordinates, our pursuit continues to translate these coordinates to native device coordinates. To reiterate our progress in the perspective of rendering, we just defined our local space with tile coordinates. Local coordinates are the coordinates of the object to be rendered relative to its local origin6. In this case, the objects are the map tiles. The next step in traditional rendering workflow is to translate object coordinates to world coordinates. This is important to understand if we are to render multiple objects in the world. If we treat all tiles in a zoom level being rendered in a single 3D horizontal plane, then the World Space has only one object. And in MapLibre Native, this plane has an origin of (0,0), positioned on the top left.
Device Coordinates
World space for MapLibre Native contains a plane in 3D with all the tiles for any specific zoom level. Map tiles are hierarchical in nature. As in they have different zoom levels. MapLibre Native internally stores a tree object that mimics a tile pyramid. However, it does not create a hierarchy of 3D planes where each plane mimics one zoom level. It reuses the same 3D plane to re-render the tiles in the requested zoom level at a time.
The journey towards rendering the tiles in the device screen from the world space starts with View Matrix, as defined in the world space. The key part here is the camera. A view matrix is a matrix that scales, rotates, and translates7 the world space from the view of the camera. To add the perspective of the camera, we apply the Projection Matrix. In MapLibre Native, a camera initialization requires map center, bearing, and pitch.
Initializing the map with a center (lon, lat) does not translate or move the 3D plane with tiles, rather moves the camera atop the defined position named center. In the rendering world, this is not the center of the 3D plane we render tiles on, rather the position of the camera.
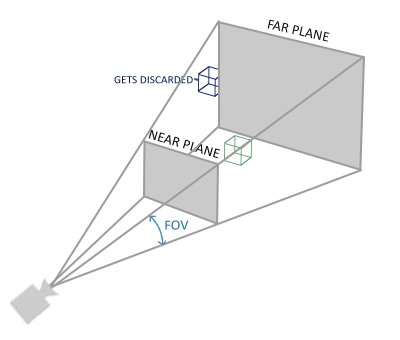 Figure 3: Perspective Frustum (Sourced from learnopengl.com)
Figure 3: Perspective Frustum (Sourced from learnopengl.com)
The benefit of tile coordinates continues here. The camera representation we use here, to be specific the view matrix, can directly take the tile coordinates to move the camera to a particular tile in a zoom level. Once a tile is built, the GPU can quickly draw the same tile with different bearing, pan, pitch, and zoom parameters8.
If we keep following Figure 2, we see we need to also add a projection
matrix. And MapLibre Native uses a perspective projection.
Perspective projection matrix introduces the sense of depth perspective
through the camera. As in objects further from the camera will look
smaller and objects closer to the camera will look bigger. This
perspective component is defined by parameter w. That is why the
shaders that MapLibre Native at the time of writing uses 4
dimensional vectors over 3 dimensional vectors. The 4^th^ dimension is
this parameter w. Therefore, theoretically a GL coordinate is of the
form (x, y, z, w).
Before we jump into the transformations, let’s revisit an example scenario:
zoom: 11.6
map center: (38.891, -77.0822)
bearing: -23.2 degrees
pitch: 45 degrees
tile: 585/783/11
On top of this, MapLibre Native uses a field of view of 36.87 degrees or 0.6435011087932844 radians. This is somewhat arbitrary. The altitude of the camera used to be defined as 1.5 screen heights above the ground. The ground is the 3D plane that paints the map tiles. The field of view is derived from the following formula:
fov = 2 * arctan((height / 2) / (height * 1.5))
Factoring only the transformations of zoom, map center, bearing, pitch, and tile in, with a viewport of 862 by 742 pixels, the projection matrix will look like9:
| x | y | z | w | |
|---|---|---|---|---|
| x | 0.224 | -0.079 | -0.026 | -0.026 |
| y | -0.096 | -0.184 | -0.062 | -0.061 |
| z | 0.000 | 0.108 | -0.036 | -0.036 |
| w | -503.244 | 1071.633 | 1469.955 | 1470.211 |
To use our tile coordinates, we will turn it to a 4D vector of (x,y,z,w) with neutral w value 1. For brevity we used z value of 0. For buildings and extrusions z value will not be 0. But this document does not cover that.
So, tile coordinate (x: 6120, y: 4151, z:0, w:1) will transform to the
following due to a vector multiplication with the projection matrix:
| x | y | z | w | |
|---|---|---|---|---|
| x = 6120 | 0.2240.224 * 6120 = 1370.88 | -0.079 * 6120 = -483.48 | -0.026 * 6120 = -159.12 | -0.026 * 6120 = -159.12 |
| z = 4151 | -0.096 * 4151 = -398.496 | -0.184 * 4151 = -763.784 | -0.062 * 4151 = -257.362 | -0.061 * 4151 = 253.311 |
| z = 0 | 0.000 * 0 = 0 | 0.108 * 0 = 0 | -0.036 * 0 = 0 | -0.036 * 0 = 0 |
| w = 1 | -503.244 * 1 = -503.244 | 1071.633 * 1 = 1071.633 | 1469.955 * 1 = 1469.955 | 1470.211 * 1 = 1470.211 |
| Final Vector | 469.14 | -175.631 | 1053.473 | 1057.78 |
The finalized vector is off from what we have expected with the result from the simulation. This is due to multiplying with low precision.
The final vector will be (x: 472.1721, y: -177.8471, z: 1052.9670, w: 1053.7176). This is not perspective normalized. Perspective
normalization happens when we divide all the components of this vector
with perspective component w.
(472.1721 / 1053.72, -177.8471 / 1053.72, 1052.9670 / 1053.72)
= (x: 0.4481, y: -0.1688, z: 0.9993)
Doing this will take us into clip space. Clip coordinates contain all
the tile coordinates we wish to render in MapLibre Native but only in
a normalized coordinate space of [-1.0, 1.0].
All that is left now is to translate this to viewport coordinates. Following Figure 2, we use viewport transform to produce these coordinates:
Pixel Coordinates: (NormalizedX * width + width / 2, height / 2 -
NormalizedY * height)
= (0.4481 * 862 + 431, 371 - (-0.1688 * 742))
= (x: 624, y: 434)
These are our viewport screen coordinates where our desired WGS84 location longitude -77.035915 and latitude 38.889814 will be rendered.
-
Clip coordinates are normalized to -1.0 to 1.0. For brevity, this document does not dive deep into 3D rendering basics. ↩
-
For brevity, this document is assuming the world we live in is three dimensional. ↩
-
For brevity, this document does not dive deep into reference ellipsoids to approximates earth, also known as Datums. EPSG:4326 or WGS84 is such a Datum or reference ellipsoid. ↩
-
There are other coordinate systems such as EPSG:54001 that uses equirectangles over squares to project the WGS84 coordinates. This document focuses on EPSG:3857 because MapLibre Native uses it by default. ↩
-
This document scopes out the trigonometric proof of this translation for brevity. To know more: https://en.wikipedia.org/wiki/Web_Mercator_projection ↩
-
For brevity, this document does not speak in depth of rendering basics in regards to coordinate systems. For more, please check: https://learnopengl.com/Getting-started/Coordinate-Systems ↩
-
Scale, rotate, and translate are common rendering transformation used to produce model, view, and projection matrices. These operations are applied right to left. As in translate first, rotate second, and scale last. Matrix multiplications are not commutative, so order of operation matters. ↩
-
The piece of code we run on GPU is called a shader. We will see more how shaders influence MapLibre Native rendering later in the document. ↩
-
Matrix and examples produced from Chris Loers work hosted in: https://chrisloer.github.io/mapbox-gl-coordinates/#11.8/38.895/-77.0757/40/60 ↩